(Updated 12/8/2017 in response to a private email asking for clarification. I still intend to create a better description and analysis, with diagrams, but hopefully these edits add enough for now..)
An n by n grid may be randomly populated with symbols, and this may be considered to constitute a private key K. By reading the rows and columns to derive the 2n words (each n symbols long) in the grid, one can create a list of 2n, n-length words, which is publicized as the public key P (after first sorting alphabetically so as to remove comprising information in the order.). Let S be the signature space, where each s ∈ S is the selection of n/2 columns and n/2 rows of K. Let F be a mapping of the message space M to S. The signer creates a signature for m∈M by computing s=F(m), and the verifier confirms by checking that each word in s is in P, and satisfies the constraints of a valid crossword puzzle.
One can imagine using a larger number of dimensions, variations using a different number of symbols, using rectangular as opposed to square grids, or using combinations of different sizes. But binary symbol spaces, a dimensionality of two, and combination size n/2 seem like reasonable choices. Mathematical validation of these parameters would be worthwhile. A significant advantage of this signature scheme is that crossword generation is known to be NP-complete.
(One would have to be very careful but, just possibly, bloom filters could be used to compress the public key at the expense of signature size. The false positive rate would have to be assessed carefully, as would the assumption that the false positives are distributed in ways inconvenient to adversaries.)
(Please notice that the signatures are intentionally revealing information about the private key and therefore, this is best suited to single-use applications, or applications where you can pregenerate a large number of keys, or applications where you can sign a new public key each time you also sign a message, or applications where the decrease in security that occurs with each signing is somehow useful in the incentives that you wish to arrange for the signer.)
Subscribe to:
Post Comments (Atom)
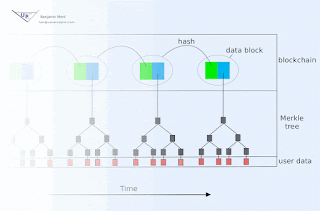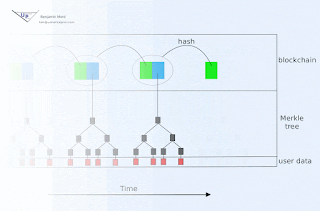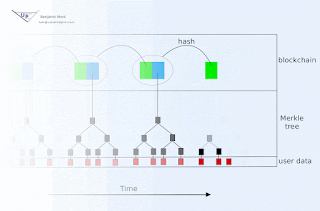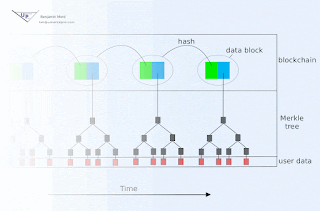
Blockchain animation
Blockchain technology offers society a new capability: sharing business records whose tamper resistance can be trusted more, and for a lo...
-
In 1976, Nobel laureate Friedrich Hayek proposed that money should be denationalized, such that privately issued moneys would compete over t...
-
The recent Ethereum hack involving a smart contract bug illustrates a type of vulnerability that we'll be seeing a lot more often. One...
-
Blockchain technology offers society a new capability: sharing business records whose tamper resistance can be trusted more, and for a lo...

No comments:
Post a Comment