Iterative hashing of a private random seed can yield keys for use in HMAC, which if revealed publicly in reverse order and on predetermined schedule, can be used in a manner similar to other asymmetric key signing protocols, where released intermediate key authenticity is verifiable in terms of its relationship to the first released (last in chain) key. The seed is like a private key, and the last of the chain (first released) is like the public key. Useful elaborations are possible, e.g. using hierarchies instead of chains.
Prior Work
Much (not all) of this appears to be equivalent to TESLA, which was published first:
https://people.eecs.berkeley.edu/~tygar/papers/TESLA_broadcast_authentication_protocol.pdf
The TESLA paper is well worth reading for several reasons. For example, it references useful related material, such as optimizations on the storage versus recomputation tradeoff for long key chains. It also points out performance advantages that I had not previously noticed, but which are especially relevant in broadcast contexts. I might rework this paper to focus exclusively on those parts which were not already included in the TESLA paper, but if anyone is aware of other prior work, I'd love to hear about it! Please comment below and/or email me at ben@mord.io
Overview
In this paper I describe a possibly novel technique, referred to here as "Delayed Chained Key Revelation" (DCKR), whereby a symmetric HMAC algorithm may be used to accomplish the following goals:
- Permit signers in possession of secret seed s to sign data
- Permit validators with timed sequential access to key series K(i) to validate these signatures
- Prevent anyone lacking knowledge of s, including validators, from forging signatures
- (Optional) cryptographically-enforce expiration of signatures (with caveat)
- (Optional) cryptographically-enforce expiration of signing authority
- Permit adhoc delegation of signing authority with predetermined cryptographically-enforced expiration, such that delegated signatures are indistinguishable from non-delegated signatures, and such that verifiers need not be aware of such delegation
- Permit adhoc hierarchical delegation structures with optional expiration points at each branch (DHKR)
- Avoid reliance on unproven mathematical assumptions beyond the preimage resistance of the selected cryptographic hash function, in defense against future quantum and classical cryptanalytic results
Motivations
Motivations for DCKR include the familiar motivations for other asymmetric signature algorithms such as RSA and DSA, since the first three goals overlap. DCKR may have additional advantages over other asymmetric algorithms, whenever one or more of goals 4-8 also apply. For example, privacy or fungibility considerations might imply that delegated signing authority must yield signatures indistinguishable from non-delegated signing authority, or else that signatures must expire. Functionary restrictions or fork resistance intended to improve governance and resist corruption might imply that signing or delegation authorities must expire on a cryptographically enforced schedule. Wallet or custodial use cases might require ad hoc yet time-constrained delegation of signing authority.
But perhaps most importantly, $100 billion market capitalizations might call for an enhanced degree of cryptographic conservatism, especially as we head into the new age of quantum computation and resulting uncertainty about the pace and nature of future cryptanalytic results. Unproven assumptions such as the computational hardness of factoring, or discrete logarithms, or R-LWE, etc inherent in other popular signature algorithms may become untenable. (Two of those three are already known to be vulnerable to quantum computation, and the third is not known to be quantum resistant to my knowledge.) The deliberate consolidation of the number of unproven mathematical assumptions underlying a cryptographically secured system may reduce the risk of breach, may expedite swapping of primitives in event of cryptanalytic surprise, and may reduce attack surface while enabling the redundant yet efficient coverage of critical system components.
It should be noted that this is not the first hash-based signature scheme proposed which is believed to be quantum resistant under assumption of cryptographic hash function preimage resistance. Lamport signatures, first proposed in 1979, are another example. Although Lamport signatures suffer various severe practical limitations, some of these have been partially or fully addressed, yielding other variants. (Perhaps I should add a comparison in an appendix.) I am however not aware of other practical hash-based signature schemes covering all of goals 1-8.
Protocol
Definitions and Basic Operation
- Let s be a securely random seed of data, known only to the signer, to serve as the private key
- Let H be a cryptographic hash function with preimage resistance
- Let K(i) be the ith iteration of H on s, such that K(0)=H(s), K(1)=H(H(s)), etc.
- Let S be a release schedule to which the signer agrees to adhere. In particular, the signer commits to never publishing K(i) prior to the time S(i). (Delays are acceptable.)
- Let S-1(t) be the inverse of S, so that S-1(t) represents the value of i scheduled for release during (or after) time interval t
- Let n be a conveniently large number (let’s defer the definition of “convenient”)
- Let K(n), with S, be known to verifiers as together comprising the signer’s public key
- Let HMAC(d,k) be a cryptographically secure signature on data d using key k, based on H (e.g. RFC 2104)
- Optional: If non-expiring signatures are desired, then let B(j) be the jth block of a chain of blocks linked by hashes in the manner first described by Satoshi Nakamoto, such that no block may be modified without altering the hashes of all subsequent blocks. (Proof of work, proof of stake etc are not necessary but also harmless to this application.)
To produce an expiring signature on data d, the signer computes HMAC(d,K(S-1(t)-1)). Notice that verifiers cannot yet verify this signature since they do not yet know K(S-1(t)-1), and the preimage resistance of H prevents them from deriving it from K(S-1(t)) or any other knowledge that they might have. They can however be assured by schedule S that, should this signature later prove valid, no one other than the signer could have produced it at the time that they first observed it.
At each time t (or earliest convenience thereafter), at least supposing anything has been signed since last publish, the signer publishes K(S-1(t)). This now enables verifiers to validate anything previously signed with K(S-1(t)) which they had previously recorded in locally-trusted tamper-resistant storage. (Because verifiers can efficiently derive child keys through iterative hashing, they can also validate any other signatures recorded during earlier time periods as well - provided that they recorded any such signatures in tamper-resistant locally trusted storage prior to first scheduled publish of their signing keys.)
Default Expiration of Signatures
Notice that if a signature using index i is first observed by a verifier at S(i) or later, then they have no assurance regarding authenticity. In a sense, the signature expired - which might be desirable or undesirable for a given use case. If they first observed and securely stored the signature prior to S(i), then they will still have assurance (regardless of when they first performed the verification itself.)
(Caveat: verifiers can render observed signatures permanent, i.e. forever provable to other verifiers, by committing them to a public tamper-resistant structure such as a public tamper-resistant blockchain. They can do this even without permission of the signer, and potentially without the signer's knowledge.)
(Caveat: verifiers can render observed signatures permanent, i.e. forever provable to other verifiers, by committing them to a public tamper-resistant structure such as a public tamper-resistant blockchain. They can do this even without permission of the signer, and potentially without the signer's knowledge.)
Rendering Signatures Permanent
If signature expiration is undesirable, then an immutable blockchain with approximately known and trustworthy block time stamps may be used to document creation of signatures prior to associated key publication. For example, HMAC(d, K) could be committed to the current block either directly or indirectly (e.g. as member of a Merkle tree whose root hash is contained within the block, perhaps by encoding within a Bitcoin transaction for example). If there is uncertainty in the timing of blocks, then the interval between signature publication must be large relative to that uncertainty.
The public blockchain in such an arrangement additionally serves to inform verifiers who were offline during relevant time intervals.
Renewable Yet Expirable Signatures
Hybrid functionality is also possible. For example, hashed data (even without signature) could be committed to a private dedicated blockchain that lacks proof of work, proof of stake or similar immutability mechanisms - and instead is secured by a signature on the most recent block that is taken to indicate authenticity and correctness of the chain. The entire chain may then be efficiently renewed just by issuing new signed blocks, or else the entire chain may be allowed to expire just by waiting for the top most block's signature to expire.
Expiration and Renewal of Signing Keys
At time S(0), the private key s expires and becomes cryptographically useless. This might be desirable or undesirable. If expiration is not desired, then the protocol could provide that at any time prior to S(0), the signer may sign some new K’(n) based on a different random seed s’, which is then understood to represent the next public key when i reaches 0. Indeed, the next K’(n) could be first publicised as early as time S(n). If desired, even multiple such K’’(n) and K’’’(n) could be advertised as early as S(n). In this way there is much flexibility in the size of n and the duration over which verifiers may first become aware of future public keys. This flexibility may be useful for example as a performance and storage optimization, so that excessively many iterations of H are not required with each signing. This may be useful for a variety of potential reasons. As one example, it could be useful in the unlikely event that dangerously large entropy loss with large n is discovered to accrue due to the “random” (or not-so-random) collisions within H.
Temporary Delegation of Signing Authority
A signer can delegate signing authority of course by handing over the private key s, just as with any signature scheme. A signer however could also delegate signing authority which automatically expires at time t, by handing over K(S-1(t)), since all earlier keys can be efficiently derived from K(S-1(t)) through simple iterative hashing.
If this feature is to be safely used, then the protocol would need to specify extra precautions around renewal of s. For example, even if published early (perhaps even time S(n)), the protocol could mandate that the new K’(n) must be signed by S(0) to be valid. In this way, anyone entrusted with advanced knowledge of K(i) for any i > 0 for purposes of delegated signing would not be able to specify a new K’’(n) for purpose of indefinitely hijacking the trust relationship.
Hierarchical delegation via DHKR
(TO DO: add diagram)
The chain of keys can be converted into a hierarchy of trees through the addition of securely random salt at each branch point. At the time of scheduled merge, the salt would then be publicly revealed by the delegatee along with the parent hash, so as to prove valid derivation.
The chain of keys can be converted into a hierarchy of trees through the addition of securely random salt at each branch point. At the time of scheduled merge, the salt would then be publicly revealed by the delegatee along with the parent hash, so as to prove valid derivation.
If there is a need to not reveal the structure or existence of delegation, then random or standardized key branches could be routinely introduced and utilized regardless of presence or absence of actual delegation, and this could be done either voluntarily or else by mandate of protocol.



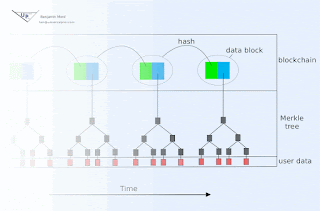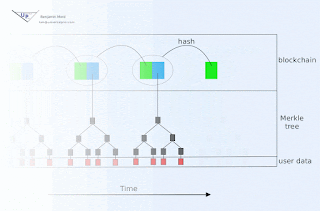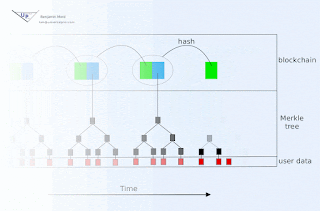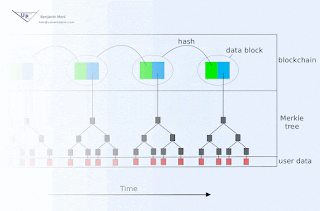
The linear portion of this might be identical to TESLA:
ReplyDeletehttps://people.eecs.berkeley.edu/~tygar/papers/TESLA_broadcast_authentication_protocol.pdf