Delayed chained key revelation for temporally asymmetric cryptography

Asymmetric cryptography is a slightly dodgy proposition today, since all known asymmetric cryptosystems require introduction of at least one additional unproven mathematical assumption. Unproven assumptions are targets, and we like to minimize target area - especially as we head into the age of quantum computation. So as to minimize this target area, can we somehow introduce useful asymmetries into more conventional symmetric cryptosystems? Why not use the dimension of time to do so? Perhaps the current knowledge of not-yet-revealed information can be leveraged into useful asymmetries.

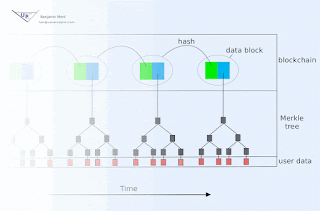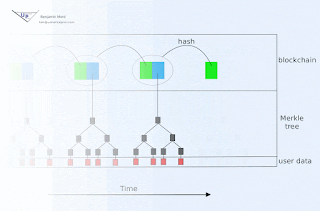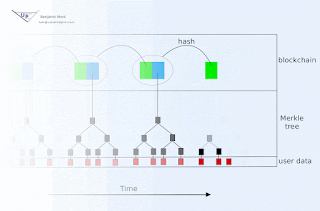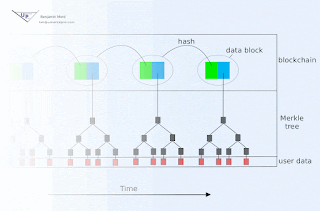
Consider, for example, a Proof of Stake algorithm with functional goals similar to Ethereum's Casper. Suppose we wish to use a symmetric signature algorithm, instead of an asymmetric cryptosystem. Before registering as a verifier, one could privately generate some securely random data, and then precompute a very long chain of n hashes using a cryptographic one-way hash function. At time of registration, only the very last of these hashes would be publicly revealed. Call that last hash H(n).

Now when signing the first block, the verifier would use H(n-2) as the signing key, and would sign the combination of the block plus H(n-1), and would additionally reveal H(n-1). When the next block is ready, the verifier would sign the combination of it with H(n-2) using H(n-3), and would publicly reveal H(n-2). Etc.

In this way, sufficiently old signatures could be verified by anyone using publicly available data. While it is true that anyone could produce a fraudulent chain of old data that would be plausible up until publication of next block, it is also true that the fraudulent chain's credibility would have to expire - since the true verifier had not revealed enough information publicly for anyone to commit future fraudulent signatures in this chain. A new participant in the network thus simply collects candidate chains, and then waits to see which (if any) maintain their plausibility past the time of collection.

I recognize this explanation might be difficult to understand without some diagrams. I apologize for that. I'll write up a more reader-friendly whitepaper in the near future. There are many parameters one could tweak, and there may be other applications. The most general concept here is simply the use of not-yet-revealed knowledge to generate other cryptographically useful asymmetries.