Conventional asymmetric cryptosystems assume computational hardness of this or that math problem (e.g. factoring, discrete logarithm, R-LWE, etc). The lack of proof of classical and quantum hardness of these math problems is what gives me pause, and is much of why I propose DCKR.
What assumption then does DCKR make for derivation of asymmetry? It assumes time travel is not possible. If anyone invents a time machine, we might have to reassess utility of DCKR as well.
(DCKR further relies on a cryptographic hash function, so irreversibility of that hash function is also necessary. But we generally rely on existence of such a function anyhow, so the goal is to not introduce additional attack points into such systems. Also, we have a larger number of hash functions to choose from - so we can more readily swap out one function for another should a vulnerability be found.)
Subscribe to:
Post Comments (Atom)
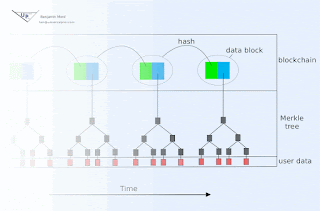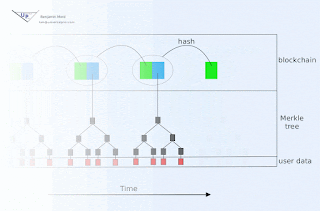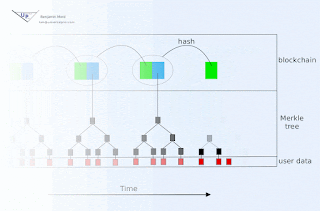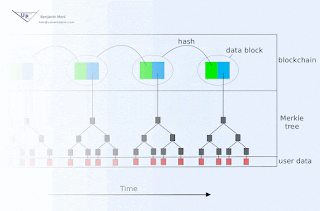
Blockchain animation
Blockchain technology offers society a new capability: sharing business records whose tamper resistance can be trusted more, and for a lo...
-
In 1976, Nobel laureate Friedrich Hayek proposed that money should be denationalized, such that privately issued moneys would compete over t...
-
The recent Ethereum hack involving a smart contract bug illustrates a type of vulnerability that we'll be seeing a lot more often. One...
-
Today's "blockchain" (acornics) technology: https://youtu.be/KP_oQHYmdRs Some blockchains today look like a larger version o...
No comments:
Post a Comment